Neural Field Convolutions by Repeated Differentiation

ACM Transactions on Graphics (SIGGRAPH Asia 2023)

We introduce an algorithm to perform efficient continuous convolution of neural fields 𝑓 by piecewise polynomial kernels 𝑔. The key idea is to convolve the sparse repeated derivative of the kernel with the repeated antiderivative of the signal.

Abstract

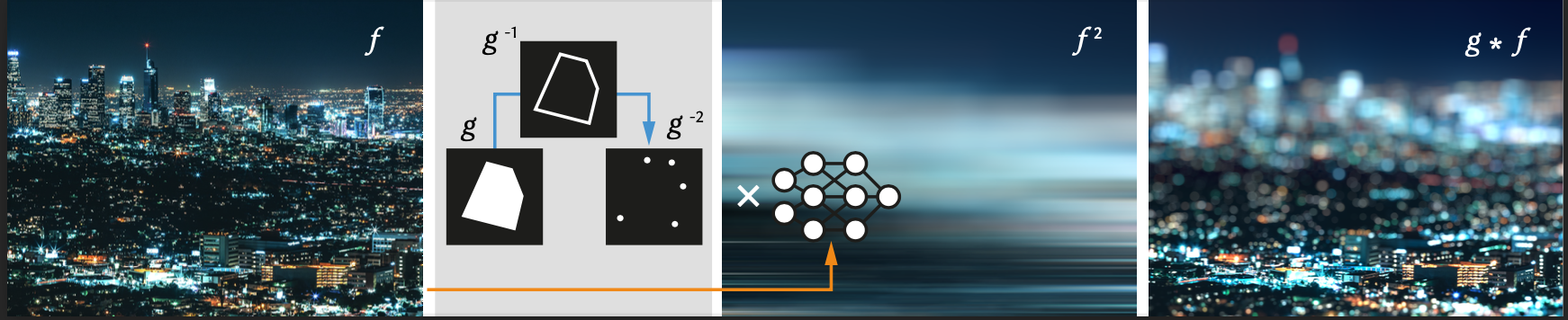
Neural fields are evolving towards a general-purpose continuous represen- tation for visual computing. Yet, despite their numerous appealing proper- ties, they are hardly amenable to signal processing. As a remedy, we present a method to perform general continuous convolutions with general continuous signals such as neural fields. Observing that piecewise polynomial kernels reduce to a sparse set of Dirac deltas after repeated differentiation, we leverage convolution identities and train a repeated integral field to efficiently execute large-scale convolutions. We demonstrate our approach on a variety of data modalities and spatially-varying kernels.